The innovative content of the solution found involves many different aspects. The algorithms have been studied to reach the highest performances in terms of adaptability, efficiency and accuracy.

REGULARISATION TECHNIQUES

Thanks to the use of a multistep propagator and interpolator the control of numerical error is guaranteed. The best step size that minimizes the error for the problem at hand is chosen with an automatic procedure. With the proper choice of regularisation techniques, we are able to improve the implemented multistep propagator/interpolator in order to be able to control the passage between different dynamical environments without loss of accuracy, resulting in a fast and reliable instrument.

Regularisation techniques allow to reduce the error by a factor of the order of 10.D+3 or more. The regularisations which provide best results are Kustanheeimo- Stiefel (KS) and Burdet- Ferrandiz (BD).

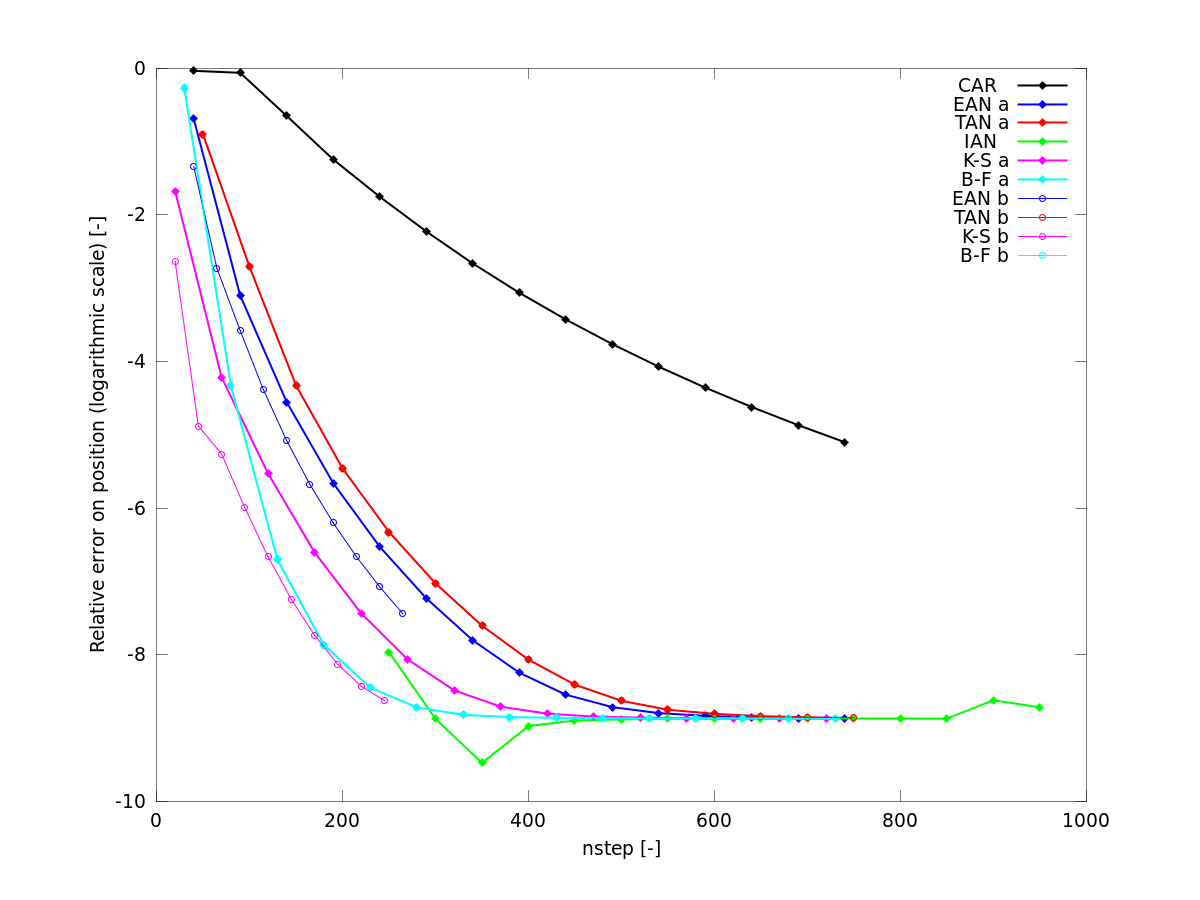
The figure shows a comparison among many different regularisations for a geocentric orbit. The perturbations activated are Earth oblateness (J2) and Moon. The orbit eccentricity is 0.7 and the perigee distance is q=6800 km. The propagation covers 50 periods. Multistep order is 8. Reference orbits are taken from Baù et al. CM&DA 116 (2013), DOI 10.1007/s10569-013-9475-x.

CLOSE APPROACHES

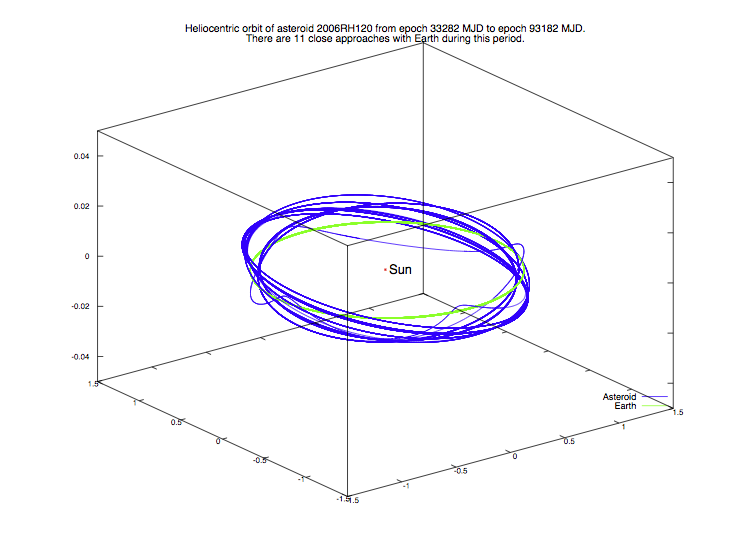
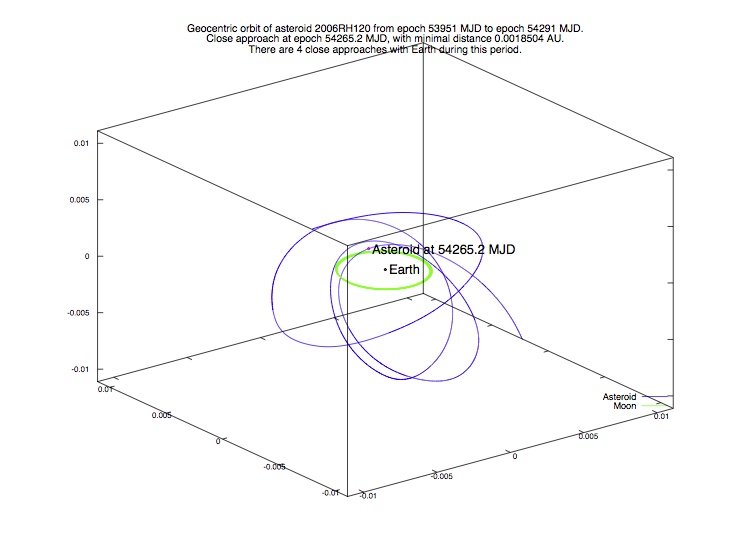
Chaotic orbits, like the ones of the Near Earth Asteroids with many close encounters with Earth, can be predicted with high accuracy over a long time span. An example of an orbit of this kind is provided by asteroid 2006RH120, which has 11 close approaches with Earth during the period from 1958 to 2007. The three last close approaches are concentrated in the year 2007.

ACCURATE COORDINATE SYSTEM CONVERTER

Singularities in the coordinate changes are managed automatically, without crashes. For relativistic coordinate changes, the transformation between different time scales is performed in a very fast and accurate way, by the creation of time ephemeris and by taking into account the station position, using the current Earth orientation data from IERS website.

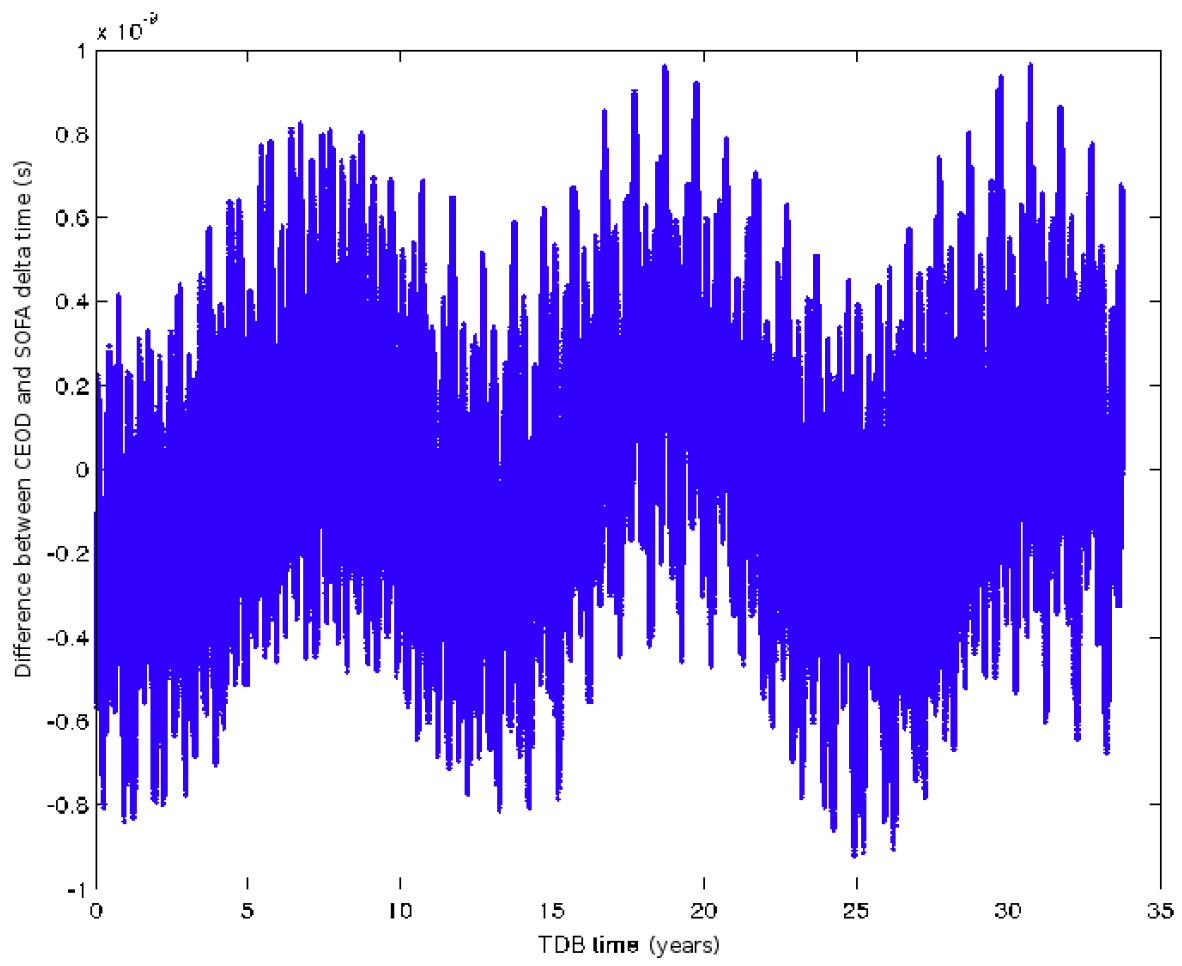
In figure absolute differences between CEOD and SOFA time scale converter (Solar System Barycentric to Terrestrial Time): differences are below 10.D-9 seconds.

FLEXIBLE TOOL

The least squares solver is designed to be as general as possible, and able to determine a very large number of parameters, both kinematic and dynamical ones, with the possibility to use linear and nonlinear constraints to treat unstable problems. The highest level of adaptability is reached by the possibility to activate different perturbations, choose different kinds of measurements and switch to relativistic dynamics, all of this by managing a single file of options.

ADVANCED SCIENTIFIC PROGRAMMING

Finally, FORTRAN2008 programming language is used, in order to exploit the latest features for parallel computing and object oriented programming.